It is the additional subscript on a mathematical array required to make relativity seem commutative instead of paradoxical. You can imagine a direction on each of the axes on a graph easily and you can imagine going in any direction in three dimensional space but it is difficult to understand there being yet another "direction" (beyond the normal sphere of directions) that can be traveled through space.
When you want to represent space you use an array. Think of it as boxes with numbers on them that we put information into. For instance a one dimensional array gives you unlimited copes of "boxes" that could hold information ( array[1] to array[bazillion]) that you can label separately but this is not very useful yet. It could, however tell you what information is at a certain place along a line. (the information we are looking for is a point)
EG: array[27] is the 27th box (or place/square on a piece of paper) that either contains a point or doesn't
Add a second dimension (subscript) to this array and now I can have unlimited set of boxes that themselves contain unlimited boxes inside them. IE: array[1][1] and array[1][bazillion] are both just boxes inside the first. This is like having the one dimensional x axis and adding the y axis. (array[x][y]) Now we've added the ability to think of directions and axes where before we really only had a line.
Now when we add a third subscript it's like we've enclosed the "array[x][y]" thing (with it's unlimited boxes inside unlimited boxes) inside yet another box which we can have an unlimited number of. and now we have a third dimension. (array[x][y][z]) We have an unlimited number of copies of two dimensional worlds.
Now you should be starting to understand that adding yet another subscript adds another axis or direction that the whole three dimensional thing can go because when we add another subscript we enclose a three dimensional world into a box which we can have unlimited copies of. There are unlimited copies of a three dimensional world we can now have.
Back to relativity:
When you have the idea that when I look at a person in motion I believe their time is occurring slower than mine and they look back at me and think my time is slower than theirs you have a paradox.
The only way to even look at this is by adding the fourth dimension. We represent the difference in time as a different "direction" or angle of travel through the fourth dimension. Typically this means that two observers in different locations have a different perspective on time and can be travelling toward the same point (through the fourth dimension) but each can feel they are moving "straight" while the other is "angled" toward them.
(This is the commonplace explanation that I personally feel has some holes, but you can see the appeal of the idea)
Creation time: Jul 20, 2014 05:10 PM PDT
It is an additional subscript on an array. It is a mathematical tool. The way to think of is is as allocated space available for things to occupy.
When you have a 1 dimensional array, there are unlimited point "slots" available to be filled. When all of them are filled it looks like a line. (of possibly unlimited length) When you have a 2 dimensional array, there are unlimited slots for 1 dimensional arrays and all the slots together are much like a sheet of paper. (of possibly unlimited size) When you have a 3 dimensional array there is space for unlimited 2 dimensional arrays like a stack of papers which can look like a cube. (of possibly unlimited size) In each case the number of slots available is the size of whatever number label you can give them. This is why three dimensions classically accounted for the whole of the conceivable physical universe.
The hard part is that when you add a 4th dimension there is space for unlimited 3 dimensional arrays and imagining that as a line of cubes is one of many very poor visualizations that don't well represent the concept. For instance, one could do the opposite and imagine every point in our universe having a hazy stack of (unlimited) additional points somehow occupying the same spatial point.
Taking this concept and adding another dimension on top of it (5th dimension) just goes beyond any reasonable visualization. One can only think of it as "unlimited 4 dimensional arrays" and so on.
Personally I use the idea of compressing and stacking, like reducing/compressing a stack of papers into one paper and then copying that stack into a stack of stacks. Repeating the process over and over each time another dimension is added. It's very poor but tends to help me wrap my head around the "stacks of stacks of stacks of stacks..." idea in general.
I hope that helps.
Check out Shiva Meucci's answer to What is a dimension? for another way of visualizing it.
Basically if you can think if it terms of boxes that could hold things then 1 dimension is a line of boxes and you can use a number label to each of them like this: array[27] and I would be referring to the 27th box and whatever it holds. So that's just a line and I'm talking about the 27th point along it.
Then you take that and make a whole new set of boxes that can hold copies of the previous set of boxes in each and every box of the new set. the easiest way to do this is basically just a stack of lines. (like a sheet of paper) So that if I referred to array[25][42] I'd mean that in box number 25 there is a whole new set of boxes related to it and I want to talk about whatever is in the 42nd box of that secondary set. This is how we get typical x,y coordinates, (array[x][y]) but it's much easier seen as a sheet of grid paper. All I have to do, instead of, for instance, trying to fit them inside each other, is I can just lay the first set out in a line on the floor one way and the second set out in lines next to the first boxes in the line. (an analogy for paper)
If I then want another set of sets of sets to add a third dimension to my array well then I can stack them on top each of the boxes on the floor and get my "z" dimension.
The problem with this method is that when I get to a fourth dimension there's nowhere left to go except maybe inside each but then the boxes are no longer really equal like they were before because they'd have to be smaller. So there’ a question of if the fourth dimension is added on the outside or inside; top or bottom of the hierarchy.
One way to visualize it now is to make copies of our big cube of boxes and just sort-of think about switching out the whole cube whenever I refer to any particular number in the fourth dimension. It's as if we have this warehouse in which we made this cube of boxes and somewhere else there are tons of copies of it and we can just request a certain numbered one of the set and men in giant forklifts will get to work changing out our cube of boxes for the one we want. Here I’ve added an exterior 4th dimension instead of an interior one.
Therefore if we start our number system at 1 then "array[1][25][42][64]" is referring to a box 25 out from the corner, 42 deep, and 64 high in our very first cube and "array[3][25][42][64]" is referring to a box in exactly the same spot after our workmen change out the whole 1st cube for the 3rd one.
NOTE:
In a previous version of this answer I failed to mention inner versus outer when adding dimensions.
In a programming language like C we’d likely start with 0 as the first one, and if you want to talk about hierarchy of what set contains the other it progresses from left to right, outer to inner.
Therefore "array[25][42][64][3]" would be referring to the 3rd slot of some weird inner space of a 3D cube. It can still be visualized in mostly the same way but it is better to make a distinction.
To visualize this we could still use the idea of multiple 3D “cubes” of boxes in various warehouses but it would be better the think of a staging area where we have this 3D grid slots a person could point at. Then when we point at 25 over, 42 away, and 64 up, we can ask for the box in that slot in warehouse 3.
I can then build whole new cubes to look at by requesting boxes from different warehouses. I can build a 3D cube that is a slice of many warehouses mixed together. This is what we do in relativity.
Creation time: Sep 04, 2014 12:56 AM PDT
When lay people say “another dimension” they are often referring to the sci-fi concept that comes from the many worlds interpretation of quantum mechanics.
They usually mean a whole other version of reality alternative to our own.
When anyone in sciences or mathematics refers to dimensions, it’s something else. Let’s talk about variables and arrays.
The best way to represent what is meant in a technical field is to talk about variables from a computer programming perspective. If you want to hold an amount that represents various things at different times you might give it a name called “ThisMonthsInterest” and then have a computer store that as something like a container to hold a number in. That’s called a variable. (and we get that name as well as most of these concepts from mathematics)
Let’s say that you have a bunch of numbers that are really similar in their use and you want to store them all together and access them easily. Then you have something like a variable but it’s a set of containers. It’s called an array and it looks like this: “MonthlyInterest[1]”
Basically, if I want to get January’s interest, all I have to do refer to the array’s name with a number attached to it that corresponds to the month and I know the number stored there is the one I want.
“Wait, why do I care about all that?”
Because we can have sets of sets! We call this a “multi-dimensional” array. If I want to keep up with multiple years of interest then I could create an array that has two numbers in it that represent the month and the year like this: “YearlyInterstDetails[2][12]”
So by using the correct numbers I can refer to the month and year and get the number I want. By storing a set of years, each of which are also a sets of months, I stored a set of sets in way I can refer to with numbers.
“Okay but why do I care about sets of sets?”
Because, to understand dimensions intuitively, you have to understand this concept of boxes of boxes intuitively.
If you haven’t seen it like this before then it should give you a different feel for x,y coordinates that are given for graphs. A sheet of graph paper can be treated like a two dimensional array called “GraphPaper[x][y]” and if I want to find out if information is in one of the boxes on the paper all I need to do is give the right numbers. Two slots or boxes over and five up would be “GraphPaper[2][5].”
The important thing to remember, however is that a one-dimensional array is just a line of containers for information, but a two-dimensional array is stack of lines of containers.
A three-dimensional array would be a box full of stacks of lines of containers. Or you could think of it as a stack of graph paper. It sounds odd because you can easily just envision a three dimensional box of boxes and think of it as one thing, but it’s important to know that there are sets within sets “under the covers” when we want to think of each individual dimension as its own thing.
Surprisingly, even classical ideas of time can be represented as 4-dimensional!
Since you can refer to anything in our world by placing a grid over everything, the world was thought of as classically three dimensional.
What if I want to refer to the whole changing world at different times? (Well, let’s just start with all the stuff moving around in a room so it feels smaller.) Then I will need a whole new set of those three-dimensional arrays. (a four-dimensional array) Sets within sets within sets…. Each new dimension expands the set.
If I want to store/represent the location of everything in the room at 3:00pm at 0 seconds then I need to store exactly where everything is at that moment. If I also want to store where everything is at 3:00pm at 1 second, then I need another whole copy of the room to say what is exactly where at that exact moment.
Therefore I can create an array called “EverythingInTheRoomOverTime[x][y][z][t]” and I can just use 4 numbers to find out what is inside a particular place in the room at a particular time. Or with a big enough number to refer to each location, everything in the world.
“Copies of the world! Oh, I see the confusion! Wait… additional dimensions?”
Yes, that means that even in a classical sense, one could store or represent a copy of the world for each successive moment in a 4D array, but each copy is a still snapshot. At this point you should see that we can just add another dimension to the array and poof, you have two or more (a set of) whole versions of reality which each has copies of each successive moment. Five dimensions can store multiple whole worlds and their every moment in a purely classical way.
“Hold it right there, buddy! You started this out saying it wasn’t whole different ‘other’ realities like laymen think! Make up your mind, pal!”
Here’s the issue. Can the whole world be totally different from one second to the next? Can everything be as it is one second and then the earth just suddenly wind up in the center of the sun with mars across the galaxy only one second later? Or even more crazy change?
Then this means there is some sort of immutable relationship between the sets. When I store where everything in the world is at a given moment with a 3D array, I could technically and mathematically store that in a 4D array right next to a world that looks completely different, but that wouldn’t be a good representation of reality because reality doesn’t just jump around from moment to moment.
This is where some of the physics of the early 20th century come in and tell us how the different parts of the sets are locked together in particular ways. Most specifically, relativity deals with this in some very interesting ways. He decided to start twisting and bending the typical grid of boxes we think of.
Maybe we could even bend and stretch them enough to tie them in a knot?
The important part is when people say “the world has x dimensions” they mean what is required, mathematically, to represent reality.
Are numerous versions of this reality existing side-by-side bound together by some weird set of rules on how they can evolve? Then I’d say we need at least 5 dimensions to represent that. Is there even more weirdness going on? Then maybe we need even more dimensions to represent it.
Creation time: Sep 12, 2017 08:55 PM PDT
Each time any physical incongruity arises you can just add another dimension to allow it to occur.
When time couldn’t be counted the same for two different users (edit: I meant “observers” but I’m leaving it in for humor) according to relativity, we just added a 4th dimension. Now this is not to say time runs differently at different speeds in different places, that could still be 3D and doesn’t require another dimension.
Relative simultaneity in relativity means it is a different time in a different place on top of the fact that times runs different speed. In a 4D universe there are infinite possible 3D configurations of reality that are reality for any given moment. (That can not be represented in a 3-dimensional mathematical structure.)
Therefore the (3D) version of the universe I experience here can be different from the universe you experience over there but it’s slightly constrained by light speed. Objects aren’t in the same places here as they are from your perspective. Therefore, if you had an exact copy of earth with the same history and placed it far enough away from this one, depending on what direction you were walking, what was happening over on that earth might be them riding around in a horse and buggy or flying around in hover cars. And technically since they can create that effect via their motion relative to you, it would have to be horse drawn carriages going one way and hover cars going the other direction.
Adding a 5th dimension allows incongruities of a 4 dimensional structure to exist side by side. This allows for infinite versions of a 4D universe to exist side by side for any given moment.
Therefore, depending on how we structured that next dimension we could possibly have all that buggy/hovercar stuff happening right here on earth. It just depends on what you are using the next higher dimension to represent. There are some conventions now established for some of the higher dimensions and that makes what I just said technically wrong compared to that “established” convention, but it’s a matter of convention. How did they establish that convention? What steps and observations were part of that process? Where’s the experiment that justifies that convention?
When you were a kid you thought the world was 3D…
Did you notice anything different when you learned it was 4D or does reality look the same with more theoretical possibilities of what could happen?
So in the end an 800 billion “D” universe might not look any different, but every sort of magical nonsense would be completely possible.
In fact, by 64D every sort of magical nonsense you could think of is likely possible and theoretically computable.
The more D you add the more incongruent reality is allowed to be mathematically. It’s a great way to fix mistakes as a mathematician. Any time you tell me my version of reality can’t do that, so long as the convention for handling the next dimension isn’t well established I can just add another dimension and say “Yes it can!”
Creation time: May 11, 2018 03:53 PM PDT
“Other dimensions” would not be “outside” our reality.
If they were completely external, then there would be no way to reach or detect them. If they were detectable that would be interaction and therefore they would be part of our reality even if a bit difficult to deal with or “reach.”
First let’s we have to briefly mention terminology: Language isn’t what is defined by some authority but what emerges culturally and, while this makes language more flexible, adaptive, and useful, it’s also fuzzier and less reliable than is ideal. This is why scientists use their own languages and terms and often think they have eliminated this problem. (they haven’t) There’s always a need for somewhat fuzzy interpretation in communication but that’s a digression for another time…
So the term “dimension” may have started to culturally mean other worlds and realities, but to scientists, mathematicians, and computer programmers it’s different. To keep from digressing too much again, it’s better to think of it as another aspect of the same reality.
I like David Bohm’s explanation of “implicate and explicate” reality that is best demonstrated visually:
Just because the dots are spread out doesn’t mean they are not still dots from a “mixed” perspective. In fact, another set of dots can be inserted after the mix and one can switch from one set of dots being unmixed to the other.
Each reality of the three dots is valid and exists but there’s many ways to slice reality.
So, what would realistic proof look like?
If we use the above model then we should see things like events occurring together in different parts of reality behaving as though they are somehow connected even though they do not appear to actually be connected.
Therefore some might say that entanglement and synchronicity would be first indications of these sorts of mechanics existing.
Even without the multiple valid interpretations of the same objects and overlapping realities like the two sets of dots described above, if reality could be unwound in the same way as that experiment, then it could be said that the past is still here in the present. General relativity tends to indicate that both the past and future have a sort of physical existence.
Therefore the fact that we have a past that impacts the present could be said to be proof of dimensions beyond three. (the fourth)
I don’t personally believe that current consensus interpretations of general relativity nor popular interpretations of quantum mechanics which deal with entanglement, are accurate enough to the underlying truth of reality to give a good picture. There’s missing additional mechanics needed. I’m a proponent of a revolution in the interpretive framework of theoretical physics that is occurring in the background and gives a much better understanding of all these concepts and many other mysteries. (without really changing the math) Hint: It’s inviscid fluid mechanical treatments…
Then there’s the many worlds interpretation.
Usually, when people think of other dimensions, they think of other separate realities and this is actually posited in the many worlds interpretation of quantum mechanics.
The fact that particles exhibit wave-particle duality which can be resolved by certain events would be seen as “evidence” for other realities splitting off from our own in this interpretation but it’s retroactive continuity in my personal opinion.
So is there some very debatable “evidence?” A little. Something concrete and reliable? No.
Creation time: Jun 21, 2018 09:15 AM PDT
(tl;dr …because it’s a reference to a tool more than to reality)
The very idea of “dimensions” are inextricably tied to historical human concepts and mental constructs.
There is no doubt that an advanced alien species wouldn’t necessarily even consider 3D reality 3 separate dimensions. We think of it as 3 separate dimensions, most recently, because of the contribution and influence of Rene Descartes we call the Cartesian coordinate system. …and before him Euclid’s “Euclidean space.”
The 3 things of “three” dimensions are a use of numbers, and though we now define spaces and shapes using numbers it used to be done the other way around. Geometry used to define math and now math defines geometry. I personally believe this flip is a negative shift in the average neurobiology of modern humans away from visiospatial reasoning and higher levels of neuronal interconnection and myelination we had in the past.
I think it’s an artifact of easier living and greater survival rates in civilization leading to genetic drift away from visiospatial intellect, but that’s a digression for another time. (If Modern Humans Are So Smart, Why Are Our Brains Shrinking?)
Either way, mathematical thought is more about linear progression/calculation and less about fuzzier (but more powerful) simultaneous analog processing. We, as a species, have gained more of the abilities of computers such as mathematical computation storage and retrieval and less of the abilities we think of as more human such as determining what math to use when, where and why. (those things computers can’t do) I’ve personally noticed that via cultural factors we’ve specialized in tool use but started losing those abilities that lead to creation of new tools, new concepts etc. This is especially true in mathematical sciences though less so in biology. (which is now advancing exponentially faster than more mathematical sciences, ironically, because of the advances of the mathematical sciences)
So another intelligent species might not think of 3D reality as fundamentally made of three things.
Therefore upgrading reality to 133.33% to have exactly “one more dimension” would look absolutely silly to that other species. It would be obvious to them that we are advancing our tool to deal with reality another way and then believing reality matches our tool instead of the other way around.
They might think of reality as made of spherical shells and only one number represents the radius of the sphere. They may fundamentally use 5 symbol categories to represent what we do with 4.
Thinking and communicating from a fundamentally geometrical basis is difficult for us to even imagine, but mathematics has been done with knots in ropes and sets of gears in the past. The numbers themselves aren’t necessarily something fundamental.
Dimensions beyond 3 are used to deal with things wholly contained inside 3 dimensions all the time.
This is crucial to understand. Additional dimensions describing this reality doesn’t mean there’s something extra to reality.
Under certain mathematical investigations, we would need to use more than 3 dimensions to be able to store and process the phenomena occuring in the image below even though it’s happening fully inside what we think of as 3D reality.
Presuming reality has a 4th dimension is literally a metaphysical assumption unsupported by experiment and can be traced from Minkowski starting in 1908 because of his interpretation of Einstein’s 1905 special relativity.
Special relativity, however, was originally hydrodynamic in the form created by its earlier developers, Poincare and Lorentz. Their version of relativistic aether has long been known to be mathematically indistinguishible from special relativity, but the meaning of the 4th dimension is completely different from how the Minkowksi convention applies it!
More information is available under their interpretation and there has never been a single experiment (considered successful) to differentiate the two or create any reason to prefer one over the other.
It bears reiteration: That preference is a culturally transmitted metaphysical assertion without experimental basis!
While the most common argument is that aether was eliminated via Occam’s razor, this is a supurbly ridiculous statement given that the replacement for a fluid is granting a single 3D moment the capability to have infininite configurations. Adding a 4th dimension is tantamount to adding infinite universes to our idea of reality. combine this with the infinite behavior of light Einstein describes and Occam’s razor clearly and unambiguously cuts the other direction.
If you’d like to more about the hydrodynamical basis of physics, this paper below was recently published:
History of the NeoClassical Interpretation of Quantum and Relativistic Physics
…and if you’d like to understand more about how and why special relativity developed the way it did then I recommend this laymen’s explanation:
Creation time: Sep 11, 2018 09:04 AM PDT
First, let’s cover the relevant meaning of extra dimensions: Additional freedom of movement.
It basically means you can move in an additional way. Think about drawing a line on a sheet of paper. The line cannot move in the third dimension. It is restricted to motion in 2 dimensions. Those two dimensions on the sheet of paper can be rolled up in the third dimension, however, to have weird arrangements such that two points that were far apart in 2D are right next to each other in 3D.
So if we have two lines that can grow at a certain speed but the same speed, we can restrict the first line to only move in 2 dimensions and it will have to travel along the rolled up sheet of paper to get to the place on the paper that was right next to where it started. If we allow the second line to go through 3D space, then it will get to the same destination almost instantly.
Because of the difference in the distances they have to traverse to get to the same point, even though the lines grow at the same speed, the additional freedom allow the 3D line access to shorter routes if they are available.
You’ve probably heard of wormhole travel. It’s the phenomena of “rolling up” 3D reality within the 4th dimension like the 2D paper within 3D reality. If there already is a wormhole, then even a 3D object can take the shorter route, but the amount of energy required to roll up 3D reality is absurd.
Now let’s use an example of something that is “4th dimensional:” light.
You’ve heard the term “light is constant” but what you probably don’t realize is that the use of this word “constant” is utterly different from how it is used with any other phenomena in the universe. It’s a reference to the idea that light travels 4 dimensionally.
You might have also heard weird things like “light speed is infinite in it’s own frame,” and been a bit confused.
The issue is that light is not just capable of using the additional freedom, it’s always using the additional freedom of movement because it exists in that higher dimension and we are only seeing a 3D slice of its existence.
If a being that only existed in 2D saw a sphere move through its plane all it would experience is a circle expanding and contracting. Theoretically this is what we see of light, a partial picture of the fuller phenomena.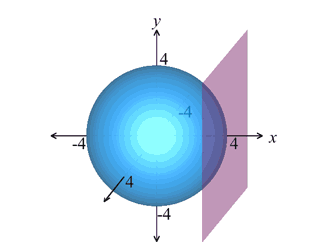
But we also can describe things like planetary orbits as 4th dimensional using this sort of visualization as well: 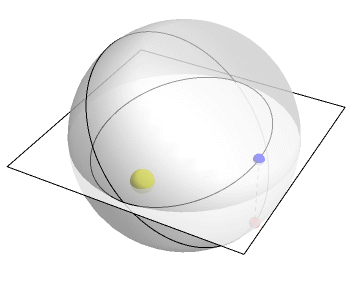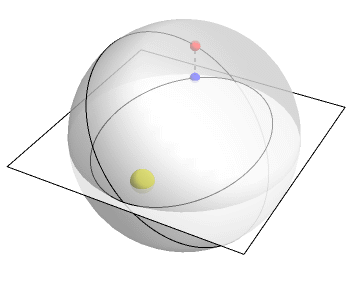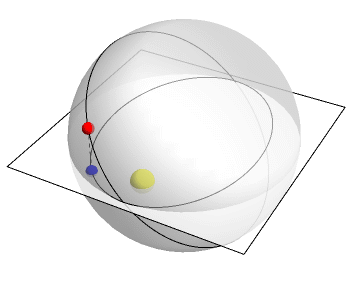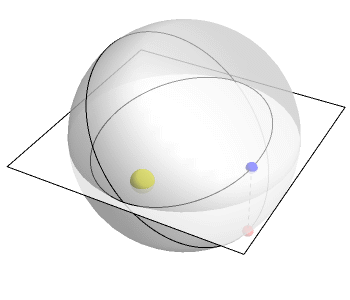
So this is, theoretically, why light can seem to go the same speed according to you, no matter how fast you go. It’s “taking a shortcut.”
When you hear “constancy” when referring to light, it means that if I put a guy on a train travelling very close to the speed of light and he passes a guy on the ground who fires a laser in the same direction, they will both see light as going the same speed according to their own perspective even though comparing those perspectives in 3D makes no sense.
IE: The guy on the train, seeing light travel light speed faster than him makes it seem like it should mean that light looks like it’s going almost 2x light speed according to the guy on the ground, but somehow it doesn’t. It seems like nonsense.
According to relativity, the two perspectives of the two travelers are actually traversing different parts of the 4D reality that light exists in.
That being said, I don’t personally believe any of it!
For instance, the final statement will only fully work in 4D if there is a preferred direction for time in the 4th dimension and therefore a preferred frame. The whole reasoning for the 4th dimension is to eliminate a preferred frame yet it still requires it.
We basically fool ourselves by making the problem too far abstracted for us to recognize the flaws. We can easily lose connection between the math and what the math physically represents because it cannot actually be physically represented.
We found a way to do what every grade school pedantic kid does when they misunderstand a word problem, set up the wrong math but solve the wrong math the right way. They believe the correct solution to the math is the correct solution to the problem and then argue with their teacher.
Now that you understand how much was added to the universe by adding a 4th dimension, let me mention Occam’s razor.
You should understand that infinite additional sheets of paper” (2D realities) can fit within 3D and therefore infinite additional 3D realities were made available to our mathematical models by adding a 4th dimension.
Because of the fact that Lorentz’s relativistic aether is not preferred but is mathematically indistinguishable from modern relativity, we say that we removed the aether because Occam’s razor demanded it.
I ask you now if simply having a difficult version of space, which provides mechanisms for all the effects we now just accept without mechanism, is “adding more” than things like infinite additional 3D realities, medium-less waves waving, and a host of other absurdities we find throughout relativity theory? If so, then we just have a vastly different and wholly incompatible view of rational thought.
Occam’s razor obviously should have cut the other direction.
Lorentz and Poincare’s solution still uses the 4th dimension as a mathematical storage for faulty information but does not propose all these skewed view of reality actually exist AS reality.
None of the weirdness or paradoxes ever even appear to occur in Lorentz-Poincare relativistic aether, yet the math is exactly the same! The simple difference is understanding the math was designed (by Lorentz, not Einstein) to represent a perspective illusion, not a new unfounded ant-mechanical irrational new view of reality.
The difference is that each individual moment of Minkowksi-Einstein space-time is completely 4D whereas Poincare-Lorentz aether simply accounts for multiple perspectives of a 3D moment of time within in a system of many individual 3D moments with faulty time-keeping.
A subtle, yet profound difference that is not mathematically discernible but is rationally separable.
If you’d like to know more:
This history paper shows how the tools of the past developed based upon aether are still around and being used and leading us toward a revolution:
History of the NeoClassical Interpretation of Quantum and Relativistic Physics
Here is an older explanation of the difference between Lorentz and Einstein relativity in given in laymen’s terms with visual aids:
And here is a recent answer I gave on quora about some of the obvious issues we have in modern physics which would, incidentally, mostly disappear under the Neoclassical interpretation.
Creation time: Oct 30, 2018 10:24 AM PDT
There is only one rational way for another “dimension” to exist.
That is via different interpretation of the same data. It should be easy to understand that in our reality a computer has whirring drives and flowing electricity and it’s all just sparks and spinning without the interpretational construct of a screen. To an AI being, a whole world could exist on top of our world through the configuration and motion of the pats in this one.
IE: Multiple realities can be stacked upon one another when you start to respect the factual nature of reality as a computational structure.
The same set of information… a plate of steel rotating to a location and electricity flowing through a wire, can also -mean- a dragon eating a knight. Therefore the cars flowing through a city and a storm passing through it could also -mean- a dragon eating a knight, in some additional universe that exists upon the computational substrate of our universe like a “virtual world.”
When you understand emergence better you realize how much more plausible this is than the pedants of yesteryear used to think.
Data can be overlapping and have multiple real meanings.
Since we can not know for sure our universe is not a simulation, we too might simply be an interpretation of the data of some deeper
The only way we would detect this universe is by trying to look at patterns within our own to see if they can create additional symmetries that play out in some abstract way. This would by no means prove their existence but it lead to additional tests etc that might go in that direction over time once we have more information.
Some people believe there is a common experience on DMT called “machine elves” in which they seem to be scientists trying to communicate with our dimension. Is the commonality of these experiences meaningful?
…I have no idea.
What I do know, is that while I’m willing to accept these possibilities, I refuse to take easy answers and quickly jump to magical interpretations of the universe.
That’s why I still strongly favor interpretations of physics that are far more mechanical and rational that commonly accepted. I don’t buy retrocausality experiments and I don’t buy spooky action at a distance. I’ve looked too closely at the experimental setups and the way the data is interpreted. It’s just experimenter bias.
I’d love for “magic” to be real. I wished very hard for it to be real all my life. But I refuse to take counterfeits like being sold to us by people very good at fooling themselves. So far, no matter how hard I search, it’s all misinterpretation and delusion.
Sure, a lot of people believe religion and the magic sold in newer physics, but it’s just not there the way they make it seem it is.
There’s some neat stuff that “feels” close to magic when we study complexity, emergence, and chaos theory, but all the non-mechanical spooky crap is just wishful thinking gone terribly awry because -now- physicists are the special people who get to wear the robes and the funny hats that prove they have the universe all figured out.
Creation time: Nov 02, 2018 09:50 AM PDT
Unfortunately, people who answer that we can “see” the 4th dimension do not understand relativity as well as they believe.
Firstly let’s clear the air and point out that Lorentz who was the originator of the first forms of the change factor, (length contraction and time-dilation in relativity) used a 4th dimension before relativity existed. It was used with the assumption of an aether-based version of space.
This use of 4th dimension is vastly different from what appears in Minkowski spacetime!
So, the commonsense idea of time composing another dimension was not new. The issue here is if a single moment of time is 4-dimensional in nature. That is the part most people will not easily understand.
From a classical standpoint, a single moment was 3-dimensional and then you needed a 4th dimension to represent the universe in every subsequent configuration that occurs moment by moment.
That is not a fundamentally 4-dimensional universe in the way it is now understood through minkowski spacetime and relative simultaneity.
There are two major ways to use and conceive of dimensions: Dividing reality or expanding reality.
A truly and fundamentally 3-dimensional reality can be divided up using multiple additional dimensions to establish interesting relationships between things. Thus when we view the experiment below, a multi-dimensional viewpoint will allow us to understand that the dots still exist in the mixed state. Their frame or reality is like another dimension from which our reality looks mixed.
Multi dimensional mathematics are used in fluid dynamics all the time and it’s just a way of keeping up with locations getting skewed and twisted around. While powerful as a tool, it’s not particularly profound or even weird, really.
…but this is just a way of dividing reality and not expanding it.
The second way to use additional dimensions like the fourth, is to allow reality to have multiple instantiations or 3D configurations that are equally valid. There are infinite possible valid configurations of a single 3D moment.
This is what is implied in Minkowski spacetime. It’s how twins can both be older than each other and many of the other paradoxes. They reside in different versions of 3D reality that are equally valid because of the 4th dimension.
From a pure programming or mathematics perspective, this is the power and usefulness of adding a dimension: Multiple possible versions of the previous dimension.
Let’s go over it one more time before moving forward.
If you have a a 2D plane it’s like a sheet of graph paper (with no thickness) that goes infinitely in x and y direction but there’s no up or down. I can mathematically represent, with some number, any place on that sheet given an origin.
If I add a 3rd dimension, now I can have an infinitely high stack of sheets of paper and can mathematically represent anywhere on any sheet of paper up or down. (like a lattice)
What I’ve done is allow for infinite possible 2D universes by adding a 3rd dimension.
If I add a fourth dimension I can now have infinite possible successive versions of a 3D reality. People who think of time conventionally or classically can grasp this as a succession of events. This idea is NOT what is conveyed by the conjoining of space and time. That is a simple division of what obviously exists and adds nothing new in degrees of freedom to a classical universe. (freedom to move up and down was granted to 2D by adding a third dimension, right?)
In minkowski spacetime, a single moment is fundamentally 4D and there are multiple moments. Each moment, however, has multiple valid 3D configurations.
How we explain relativity and relative simultaneity, it is the succession of events that is no longer in a specific relation without reference to location.
Unfortunately at this point to go further I would have to invoke Kaluza-Klien and start talking about the necessity of a 5th dimension to really represent reality over time in a relativistic universe, but let’s save that for a different question (and heated argument).
So can we visually see the 4th dimension? No!
A single particle of light, however, experiences all of the time of its traversal at once so if you were a massless particle that could travel the speed of light, then possibly sort-of yes.
How can we prove additional dimensions?
That may be impossible. We can prove the usefulness of multi-dimensional treatments of a field by placing multiple particles in seemingly disconnected places and then showing that our predictions will cause them to wind up in some specific pattern that shows the starting points actually were associated in some way by the distribution of forces etc…
Unfortunately that only proves that divisions of reality are a useful mathematical tool. To prove there is more to reality we must prove something else.
The exception is entanglement. If entanglement is a real effect and most people do believe it is, (though I agree with Einstein that it’s experimenter effect) then the connection between parts of reality in such a manner would prove that signals need not move through space because there is no space between them in these additional dimensions.
Here’s how to understand it.
If you’re a fundamentally two-dimensional creature then a dot on a page which is a location in your universe cannot be connected to some other point further away on the page. If you’re a 3 dimensional creature you know that all you must do is fold the sheet over and two locations that seem far away on the x or y axis are right next together and even touching, on the z axis. Those supposedly distant locations can directly and mechanically interact.
Additional dimensions allow our 3D universe to be already naturally “folded” or twisted and mixed in just such a manner so that distant places may factually be right next to each other in this larger reality.
The idea that entanglement works supports such a view from an experimental evidence standpoint.
That said…
I personally disagree with the experimental setups and the interpretation of the events that are factually measured. I do not disagree that there are observations that are reliable, I just disagree with what they mean. I see fundamental errors in their reasoning.
I also don’t disagree that toast can be burnt to look like Jesus; I just don’t think it’s supernatural. There are fundamental errors in the reasoning.
Evidence relies quite strongly upon interpretation.
Creation time: Feb 18, 2019 08:38 PM PST